Fabric From First Principles

⚠️ This is a draft post. Read at your own risk!

Introduction

So I just got bored and then I decided to start some kind of a new hobby. The aim was to monthly, take a random paper on physics, or mathematics, and try to implement it and visualise it. Since I am too busy to continue work on my bigger projects, I thought this is a good way to keep in touch.

Anyways, the first paper I chose is Simulation of Clothing with Folds and Wrinkles. Another thing I will do is to try my best to derive the equations from the first principles of physics, which in this context, is Newton's laws of motion.

Setup

I will be using raylib for the rendering, and odin for the programming language (apologies for no syntax highting). So the first thing is to setup a "cloth", and that for now, will be just particles connected by triangles.

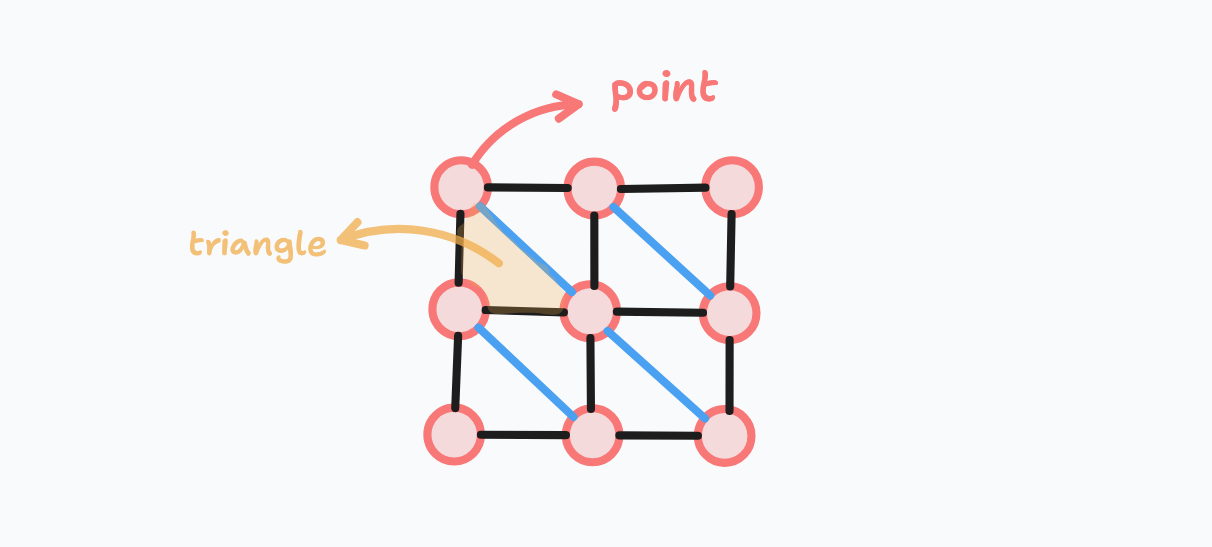
Structs for the particles and triangles are as follows:

01Particle :: struct {
02	position:    rl.Vector3,
03	velocity:    rl.Vector3,
04	forced:      rl.Vector3,
05	mass:        f32,
06	inverseMass: f32,
07	fixed:       bool,
08	index:       i32,
09	color:       rl.Color,
10}
11
12Triangle :: struct {
13	particles: [3]i32,
14	normal:    rl.Vector3,
15	area:      f32,
16}

After that I just created a basic function, that generates a mesh and draws it. This is what I have for now.

Force on each particle

Before deriving, I will just be describing the most basic laws and rules, so that the reader and I are on the same page.

The Groundwork

So cloth simulation, just like every other newtonian system, is based on the laws of motion. The first law, or the law of interia mathematicaly states that:

\sum F=0 \Rightarrow \frac{dv}{dt}=0

In layman terms, if there is no force acting on an object, there is no change in its velocity.

The second law, or the law of acceleration, states that:

F=ma = m \frac{dv}{dt} = m \frac{d^2x}{dt^2}

This implies that the acceleration of an object is directly proportional to the net force acting on it, and inversely proportional to its mass.

The third law simply states that for every action, there is an equal and opposite reaction.

Another critical law in physics is the law of conservation of energy, which states that energy remains constant over time in a closed system. When it comes to cloth simulation, we will consider

Kinetic Energy, which is the energy of motion, and is given by the formula:

KE = \frac{1}{2}mv^2

Potential Energy, which in this case, instead of being configured by gravity and height, will be configured by a spring constant and the displacement. The formula is:

PE = \frac{1}{2}kx^2

Where $$k$$ is the spring constant, and $ x $ is the displacement from the rest position.

For a single particle, the total force acting on it is given by:

F = F_{internal} + F_{external}

Where $F_{internal}$ is the force acting on the particle due to the other particles, and $F_{external}$ is the force acting on the particle due to external factors, such as gravity, other particles, wind, etc.

Mass Spring System

The foundation of cloth simulation is based on the belief that each particle on the cloth is connected to its neighbours by springs. According to Hooke's Law, the force exerted by a spring is given by

F = -k(x - x_0)\hat{e}

Where $$k$$ is the spring constant (akin to stiffness here), $$x$$ is the current length of the spring, $$x_0$$ is the rest length of the spring (natural length) and $\hat{e}$ is the unit vector in the direction of the spring.

Let us say we have two particles, $$i$$ and $$j$$ at positions $\vec{x_i}$ and $\vec{x_j}$ , connected by spring. Then $\hat{e}$ can be calculated as $\vec{x_j} - \vec{x_i}$ divided by the modulus of the same, which gives the length of the spring.

\hat{e} = \frac{\vec{x_j} - \vec{x_i}}{|\vec{x_j} - \vec{x_i}|}

Substitute $\vec{x_j} - \vec{x_i}$ by $r_{ij}$ and $|\vec{x_j} - \vec{x_i}|$ by $$l$$ , we get:

F_i = k(l - l_0) \frac{r_{ij}}{l}

and using Newton's third law, we can express the force on particle $$j$$ as:

\[ F_j = -F_i \]

This would be the most simplest form of a cloth model. If you want to do a rigorous derivation of this formula, keep in mind that force is just the negative gradient of the potential energy. So we can write:

F_i = -\nabla V_{spring}(\mathbf{x}_i, \mathbf{x}_j)

Where $V_{spring}$ is the potential energy of the spring, which is already mentioned above.

Non Linear Springs

But real clothes exhibit non-linear elastic behaviour. One of the easier ways is to use the strain limiting model, which basically says

V_{\text{strain-limited}}(\mathbf{x}_i, \mathbf{x}_j) =\begin{cases} \frac{1}{2} k (l_{\text{max}} - l_0)^2, & \text{if } l > l_{\text{max}} \\ \frac{1}{2} k (l - l_0)^2, & \text{if } l_{\text{min}} \leq l \leq l_{\text{max}} \\ \frac{1}{2} k (l_{\text{min}} - l_0)^2, & \text{if } l < l_{\text{min}} \end{cases}

In programmer terms, it basically means we are clamping the length of the spring to a maximum and minimum value. This is done to prevent the spring from stretching too much or compressing too much, which would result in unrealistic behaviour.

For our simulation we will use the above but there are even more realistic models, such as the exponential spring model, which is given by:

V_{\text{exp}}(\mathbf{x}_i, \mathbf{x}_j) = \frac{k l_0^2}{4 \alpha^2} (e^{\alpha \epsilon} + e^{-\beta \epsilon} - 2)

Where:

$\epsilon = (l - l_0) / l_0$ is the strain
$\alpha$ controls the stiffening behavior under tension
$\beta$ controls the softening behavior under compression

Gravity and PE Calculation

The potential energy due to gravity (not spring this time) is given by:

V_{gravity}(x_i) = mg(x_i)

Therefore, the total potential energy of the system is given by:

V_{total} = \sum_i V_{spring}(\mathbf{x}_i, \mathbf{x}_j) + \sum_i V_{gravity}(x_i)

Where $V_{spring}$ is the potential energy of the spring, and $V_{gravity}$ is the potential energy due to gravity.

Spring Types

A cloth mesh, typically contains three types of springs:

Structural Springs: These are the springs that connect the particles in the same row and column. They are responsible for the overall shape of the cloth.
Shear Springs: These are the springs that connect the particles diagonally. They are responsible for the shear deformation of the cloth.
Bending Springs: These are the springs that connect the particles that are two rows or two columns apart. They are responsible for the bending deformation of the cloth.

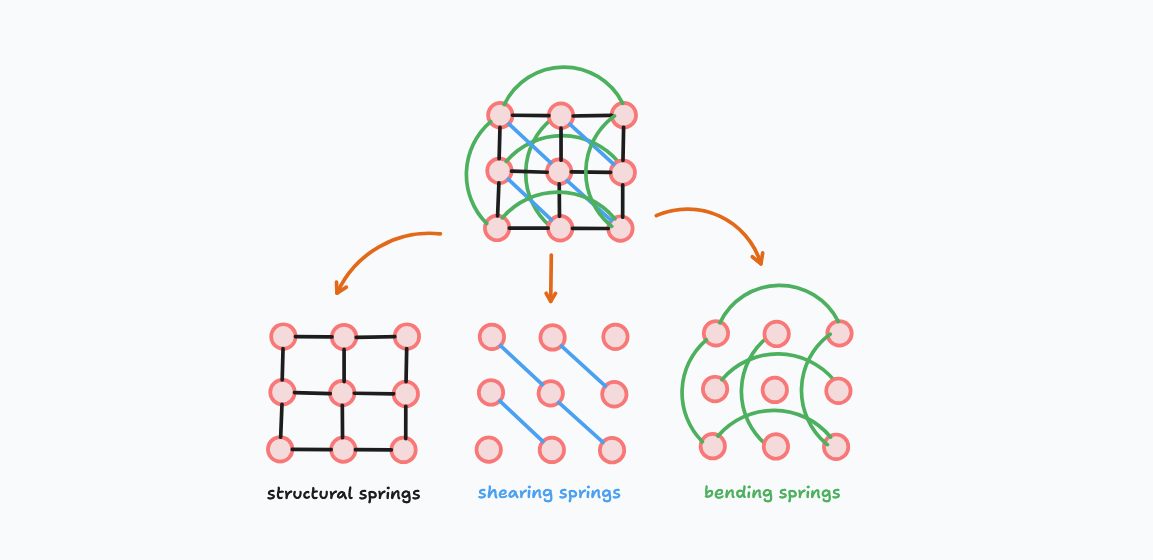
springs

For different types of springs, we can just swap the spring constant $$k$$ for each type. Each spring will have its own spring constant, $k_{struct}$ , $k_{shear}$ and $k_{bend}$ .

Bending Model

While the simple bending springs provide basic resistance to bending, a more physically accurate model uses the dihedral angle between adjacent triangular faces. For two triangles sharing an edge, we define a bending energy as:

V_{bend} = \frac{1}{2} k_{bend} (\theta - \theta_0)^2

Where $\theta$ is the dihedral angle between the two triangles, and $\theta_0$ is the rest angle (usually $\pi$ ). The force on each particle can be derived from this energy, similar to the spring forces.

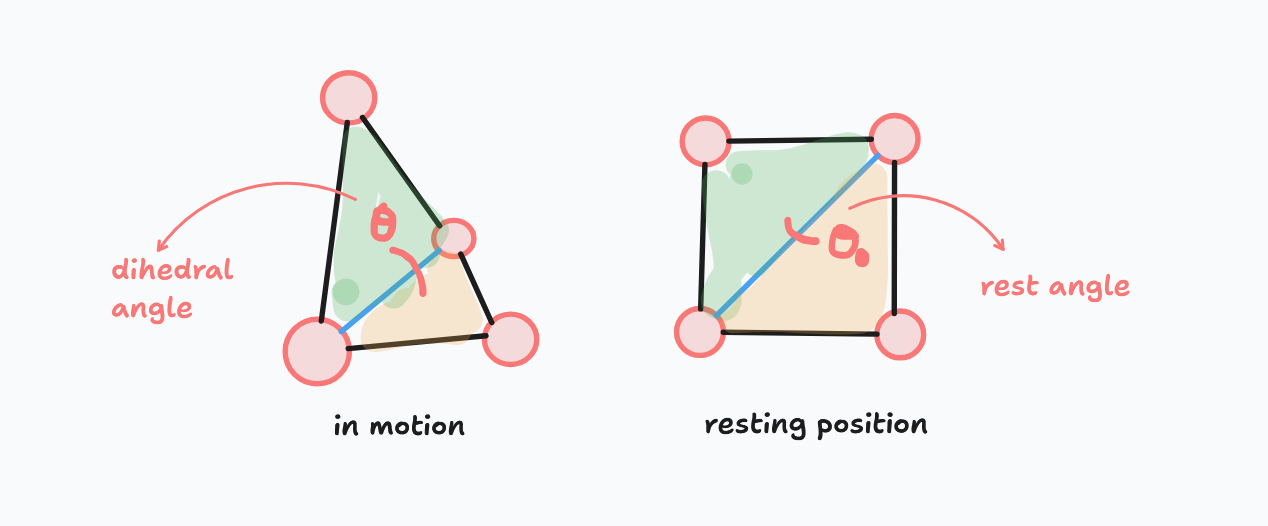
dihedral

The dihedral angle is the angle between the two planes formed by the triangles. It can be calculated using the normal vectors of the two triangles. For two triangles with vertices $$x_1$$ , $$x_2$$ , $$x_3$$ and $$x_4$$ , where $$x_1$$ and $$x_2$$ are the vertices of the shared edge, the dihedral angle can be calculated as:

cos(\theta) = \frac{n_1 \cdot n_2}{|n_1||n_2|}

where $n_1 = (x_2 - x_1) \times (x_3 - x_1)$ and $n_2 = (x_4 - x_1) \times (x_3 - x_1)$ are the normal vectors of the two triangles.

The force can, like always be derived as the negative gradient of the potential energy.

Damping

In a real piece of cloth, the energy is dissipated through various mechanisms, leading to damping. The simplest model is velocity-proportional damping

F_{damping} = -c v

A more accurate model applies damping to the relative velocity of the particles connected by a spring:

F_{damping,i} = -c[(v_j - v_i) \cdot e_{ij}]e_{ij}

Where $$c$$ is the damping coefficient, $$v_i$$ and $$v_j$$ are the velocities of the two particles connected by the spring and $e_{ij}$ is the unit vector in the direction of the spring. The dot product $(v_j - v_i) \cdot e_{ij}$ gives the relative velocity along the spring direction.

Now after all of these calculations, we can finally write the force on each particle as:

F_i = F_{spring,i} + F_{gravity,i} + F_{spring-damping,i} + F_{external_i}

where $F_{spring}$ is the force due to the springs, $F_{gravity}$ is the force due to gravity, $F_{damping}$ is the force due to damping and $F_{external}$ is the force I will apply to the cloth, such as wind or cursor movement.

to be continued... time step, time integration, constraints, collisions

12 May 2025