Animating Mascots

Introduction

not a tutorial, just a devlog

Okay, here is the core idea: I suck at art, and I suck at animations, and AI art is going to make me look like a villain, so fine, I'll do it myself, with maths. Take the mascots of programming languages, try to draw them with basic shapes as much as possible, and animate them with procedural animation. The first one would be python, then ferris, golang's gopher and might just even do zig, I really do not know, this intro is just my concious stream of thought. I will yet again use Odin and raylib for this.

Procedural Animation

Procedural animation is interesting because it takes away the idea of a "keyframe" and instead the position and state of the object is determined by a function. This means that you can have a lot of objects moving around and interacting with each other without having to worry about the details of how they move. You can just define the rules and let the computer do the rest.

Constraint

The most basic example of constraint would be just to have 2 balls and make one of them follow the other by a fixed distance constraint.

In this example, the red ball is the leader and the blue ball is the follower. We first calculate the distance between the two balls, normalize the vector and then set the distance between the two balls.

1points[1].position.x = points[0].position.x + direction.x * constraint_length
2points[1].position.y = points[0].position.y + direction.y * constraint_length

Chained Constraint

The idea, is to add more points and make them follow the leader, and in some sense, making a chain of balls, which is a good start for a snake.

So before proceeding, I defined some structs to represent the points and the body of the snake.

1Point :: struct {
2    position: rl.Vector2,
3    velocity: rl.Vector2,
4    radius: f32,
5}
6
7Snake :: struct {
8    segments: [dynamic]Point,
9}

So to make it look like a chain, we want each ball to follow the previous ball, for now the head will be going in a random direction. We just calculate the direction of the previous ball, get the distance between them, normalize the direction and update it like we are used to doing, but now just inside a for loop.

01for i := 1; i < len(snake.segments); i += 1 {
02      direction := rl.Vector2 {
03          snake.segments[i].position.x - snake.segments[i-1].position.x,
04          snake.segments[i].position.y - snake.segments[i-1].position.y,
05      }
06      
07      current_distance := math.sqrt(direction.x * direction.x + direction.y * direction.y)
08      
09      if current_distance > 0 {
10          direction.x /= current_distance
11          direction.y /= current_distance
12      }
13      
14      snake.segments[i].position.x = snake.segments[i-1].position.x + direction.x * snake.segment_distance
15      snake.segments[i].position.y = snake.segments[i-1].position.y + direction.y * snake.segment_distance
16  }

And then we can make a function to add more segments to the snake, so as to not have a really small snake. The next thing is to instead of randomly changing the direction of the head every 2 seconds, we give it a random point to go to, this makes it clearer in the demonstration as to what is happening.

The most obvious problem here is that the snake is collapsing on itself, and that is because there is no limit to how much the head can turn.

todo

Makeup

For now, let just upgrade the body of our snake from a bunch of balls to something that looks more like a snake. The first approach, draw two points at the end of the diameters of the balls, and draw lines between them. Which diameters? The ones that are perpendicular to the direction of the ball.

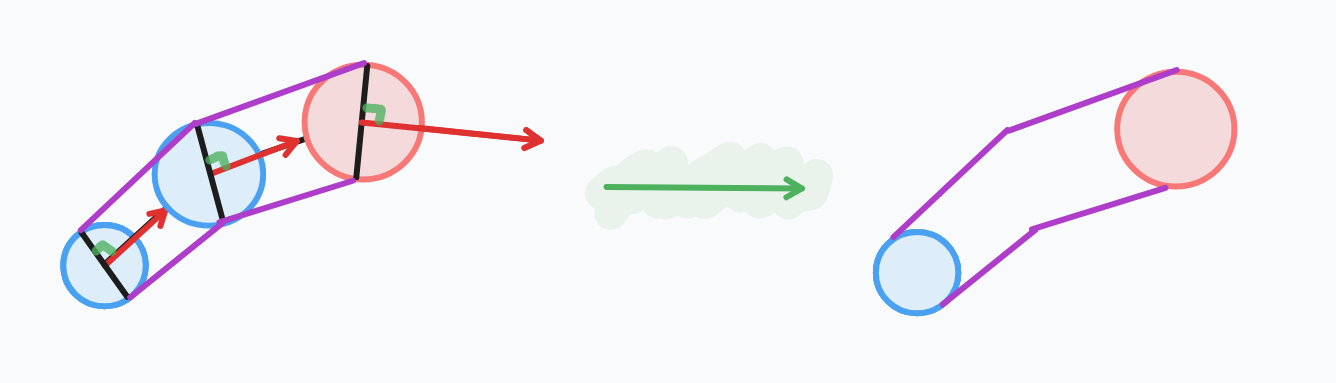
So in the drawing function for snake, we get the perpendicular vector of the direction of the ball, and then we calculate the left and right points of the ball by:

1left_point := rl.Vector2{
2  curr.position.x + perp.x * curr.radius,
3  curr.position.y + perp.y * curr.radius,
4}
5
6right_point := rl.Vector2{
7  curr.position.x - perp.x * curr.radius,
8  curr.position.y - perp.y * curr.radius,
9}

curr is the current ball in a for loop, and perp is the perpendicular vector.

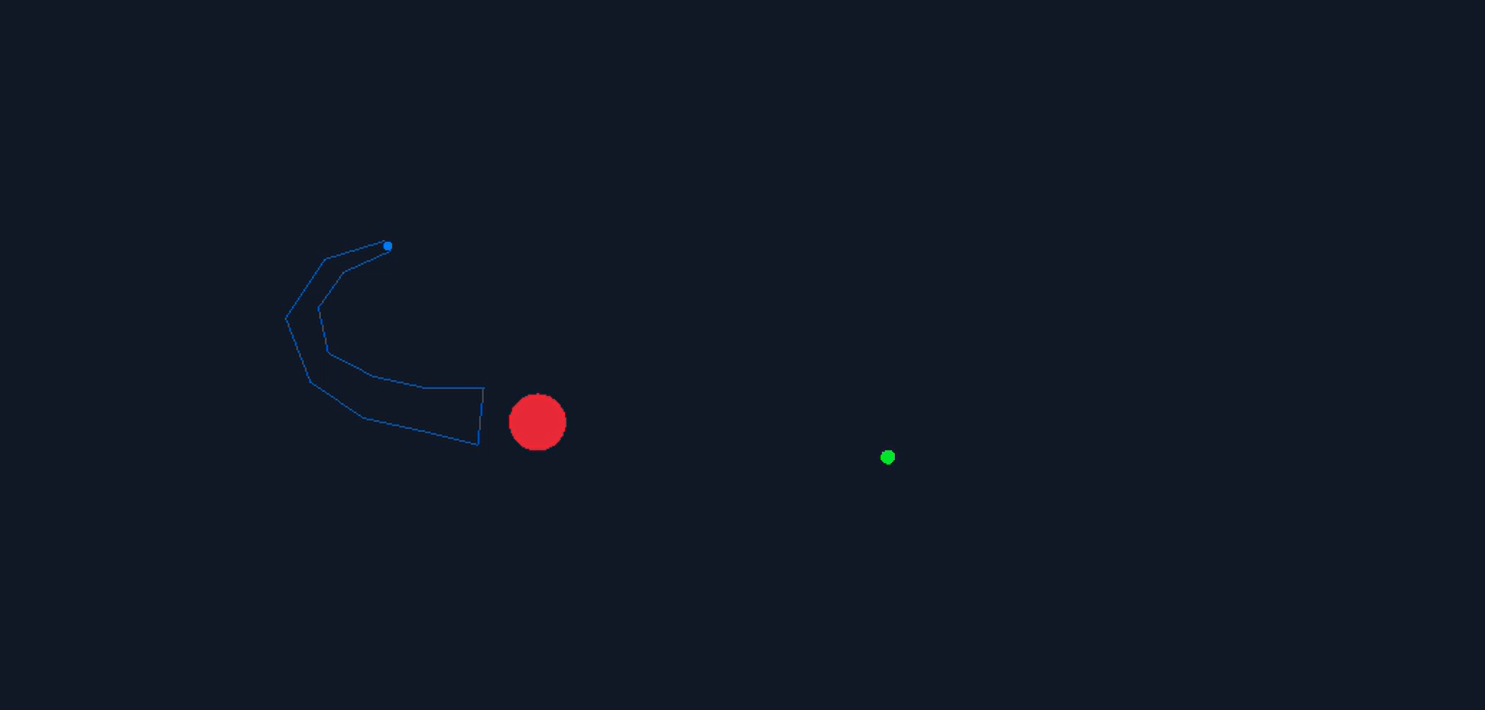
Here is how far I got with this approach, and yes it is kinda bugged, but we do notice the actual problem with this, the snake looks unnatural because of the number of straight lines. So we need to add some curves to the snake and there are a bunch of ways to get to this. One approach is to use the bezier curve, but in bezier curves, there are no points of local control, i.e if you reposition any one point, no matter how far from the other points, it will change the whole curve. Add to that, the fact that bezier curves are not computationally cheap. Therefore we resort to something called splines.

Even though splines are a topic that deserve a whole devlog on their own, I cannot do it justice within this one. But if you want to learn more about splines, I highly recommend watching this video.

For my snake, I will be using Catmull-Rom splines because they are staple in game development, and also because raylib has a function for it.

To be continued